Integral
I
Die LEIBNIZ´sche Schreibweise des lang gezogenen S für das Integralzeichen führt nicht selten zur Interpretation Integrieren bedeutet Summieren. Dabei wird als Einstiegsmodell meist der Flächeninhalt zwischen dem Graphen der Funktion f(x) = x2 und der x-Achse in einem Intervall [0; a] durch Ein- bzw. Umschreiben von Rechteckstreifen (Stichwort Unter- und Obersumme) angenähert und mit Hilfe des Integrals exakt berechnet.
Dem lateinischen Ursprung nach bedeutet das Wort integrare "wiederherstellen". Es geht also in erster Linie um das Rekonstruieren einer Funktion, womit das Integrieren auch als Rekonstruieren bezeichnet werden kann.
Als möglicher und durchaus geeigneter Einstieg in die Materie der Integralrechnung erweist sich dabei das legendäre Badewannenbeispiel:
In eine leere Badewanne wird fünf Minuten lang Wasser mit einer konstanten Fließgeschwindigkeit von 10 Liter/Minute eingelassen.
Anschließend wird die Wasserzufuhr gestoppt und das eingelassene Wasser fünf Minuten lang durch den Abfluss, der eine Fließgeschwindigkeit von 5 Liter/Minute ermöglicht, geleitet.
Bezeichnet man mit x die Minuten nach Beginn der Wasserzufuhr und mit f(x) die Zuflussgeschwindigkeit zum Zeitpunkt x, so besitzt die Funktion f(x) im Intervall [0; 5] den konstanten Wert 10 und im Intervall [5; 10] den konstanten Wert -5 (eine Abflussgeschwindigkeit besitzt bei einer derart gewählten Funktion f(x) ein negatives Vorzeichen).
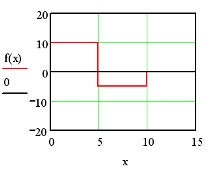
Für einen Zeitpunkt x1 während der Zuflussphase [0;5] ist die bis zu diesem Zeitpunkt zugeflossene Wassermenge gleich dem Produkt 10.x1 Liter. Dies entspricht zugleich dem Flächeninhalt zwischen der Funktion f(x) und der x-Achse im Intervall [0; x1].
Für einen Zeitpunkt x2 während der Abflussphase [5; 10] ist hingegen von den bis zum Zeitpunkt x = 5 Minuten eingelaufenen 50 Litern jene Wassermenge abzuziehen, die bis zum Zeitpunkt x2 wiederum abgeflossen ist, d.h. vom Inhalt des Rechtecks oberhalb der Zeitachse ist der Inhalt des unterhalb der Zeitachse liegenden Flächenstückes im Intervall [5; x2] zu subtrahieren.
Dadurch ergibt sich fast zwangsläufig, dass in der Integralrechnung unterhalb der waagrechten Achse liegende Flächenstücke mit negativem Vorzeichen zu versehen sind.
Somit erhält man für die Volumsfunktion V(x), die jedem nicht negativen Zeitpunkt x die augenblicklich in der Badewanne vorhandene Wassermenge zuordnet:
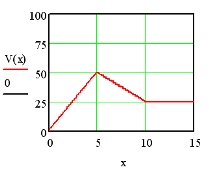
Ist nun die Zuflussgeschwindigkeit nicht konstant, aber z.B. gleichmäßig wachsend, so besitzt die Funktion f(x) während der Zuflussphase den Wert 2x. Wiederum entspricht die zu einem Zeitpunkt x1 der Zuflussphase eingelassene Wassermenge dem Flächeninhalt zwischen der Funktion f(x) und der x-Achse im Intervall [0; x1]:
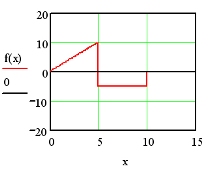
In diesem Fall kann der gesuchte Wert x12 leicht mit Hilfe der Flächenformel eines rechtwinkeligen Dreiecks überprüft werden.
Für die Volumsformel V(x) ergibt sich dadurch folgendes Schaubild:
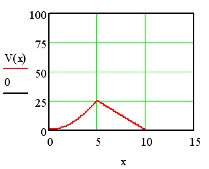
Besitzen jedoch Zufluss- und Abflussgeschwindigkeit einen Verlauf, der der Funktion f(x) = (1/128)x4 - (3/16)x3 + (15/16)x2 + (3/2)x entspricht, so ergeben sich folgende Schaubilder:
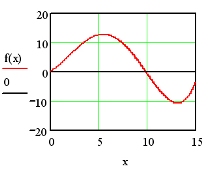
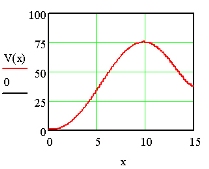
Abschließend sei anhand eines Beispieles noch auf die Interpretation Integrieren bedeutet Mitteln hingewiesen.
Im Laufe eines Tages wird zwischen a = 6 Uhr und b = 18 Uhr mehrfach eine Außentemperatur gemessen.
Bei der Frage nach der mittleren Tagestemperatur ist die Verwendung des arithmetischen Mittelwertes zwar nahe liegend, aber nicht unproblematisch, da zum einen die Temperatur zwischen zwei Aufzeichnungspunkten nicht konstant ist und die Abstände zwischen zwei Messungszeitpunkten nicht gleich lang sind.
Die Verwendung des gewogenen arithmetischen Mittelwertes
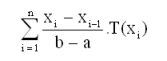 ,
,bei dem jeder gemessene Temperaturwert T(xi) mit dem Anteil, den das Zeitintervall [xi-1; xi] am gesamten Messungszeitraum [a; b] besitzt, gewichtet wird, kommt der gesuchten Antwort deutlich näher und wird einen umso verlässlicheren Wert für die mittlere Tagestemperatur liefern, je mehr Messpunkte verwendet werden.
Besitzt man nun dank eines automatischen Temperaturschreibers einen stetigen Temperaturverlauf T(x) während des gesamten Beobachtungszeitraumes [a; b], so strebt der Ausdruck
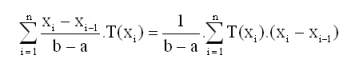
für n gegen ∞ (d.h. für beliebig viele Messpunkte) gegen den Wert
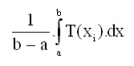
Somit kann das Integral einer stetigen Temperaturfunktion T(x) auch als Mittelwert (genauer: verallgemeinerter arithmetischer Mittelwert) interpretiert werden.