Das HERON´sche Verfahren
Mit Hilfe des nach HERON von Alexandria (um 60 n. Chr.) benannten Verfahrens ist es möglich, die Quadratwurzel einer positiven Zahl ausschließlich mit Hilfe der elementaren Grundrechenoperationen zu ermitteln. Das Verfahren liefert schrittweise immer bessere Näherungen für den Wert √a.
Um nun den Wert √a näherungsweise zu ermitteln, werden folgende drei Schritte benötigt:
| Beschreibung | Beispiel √17 | |
|---|---|---|
| 1. Schritt | Festlegen einer ersten Näherung x1 mit x1 > √a. | x1 = 5, da 42 = 16 und 52 = 25. |
| 2. Schritt | Berechnen des Ausdrucks (a/x1). | a/x1 = 17/5 = 3,4 |
| 3. Schritt | Berechnen des arithmetischen Mittels aus den beiden Werten x1 und a/x1. | 1/2 ⋅ (x1 + a/x1) = 4,2 |
Das gebildete arithmetische Mittel wird mit x2 bezeichnet und ist ein besserer Näherungswert für den gesuchten Ausdruck √a, denn es gilt:
Aufgrund der Voraussetzung
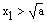
ergibt sich für die Kehrwerte
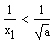
und durch Multiplikation mit dem Faktor a (> 0) die Gleichung:
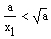
Da das geometrische Mittel zweier Zahlen niemals größer als das entsprechende arithmetische Mittel sein kann, gilt ferner:
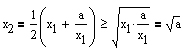
Zusätzlich erhält man aus der Voraussetzung
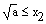
durch Quadrieren die Gleichung
a ≤ x22
und damit:
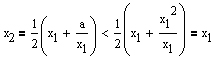
Somit ergibt sich insgesamt:
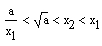
Für das Beispiel √17 gilt bekanntlich:
| 1. Näherung | x1 = 5 |
| 2. Näherung | x2 = 4,2 |
Nun können die obigen Schritte stets wiederholt werden, indem das arithmetische Mittel aus den jeweiligen Näherungswerten gebildet wird, d.h. es gilt
| Beschreibung | Beispiel √17 |
|---|---|
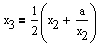 |
x3 = 4,1238095 |
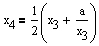 |
x4 = 4,1231057 |
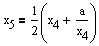 |
x5 = 4,1231056 |
und allgemein:
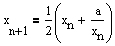
Das HERON´sche Verfahren kann durch Verallgemeinerung zu einem Näherungsverfahren für die k-te Wurzel einer (nicht negativen) Zahl a ausgebaut werden.
In diesem Fall gilt bei Verwendung einer ersten Näherung die Gleichung
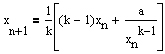 .
.