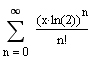Logische Fortsetzung
In vielen Rätselecken findet sich die Zahlenreihe
1
2
4
?
Bei den meisten Zahlenrätseln wird im allgemeinen folgende Begründung gegeben:
Die Reihenfolge der Zahlen gehorcht einer bestimmten Funktionsgleichung, in die die natürlichen Zahlen − meist mit 1 beginnend − fortlaufend eingesetzt werden.
Für die logische Fortsetzung der eingangs zitierten Zahlenreihe <2, 4, 8, ...> wird meist das Bildungsgesetz f(x) = 2x verwendet.
Gleichzeitig entsteht in diesem Fall eine geometrische Folge, da jedes neue Folgenglied durch Verdoppeln des vorherigen Folgengliedes gebildet wird.
Somit lautet die "logische" Fortsetzung 16.
Das Bildungsgesetz f(x) = 2x ist aber keineswegs das einzige, das die Zahlenreihe <2, 4, 8, ...> erzeugt.
Wird nämlich das Bildungsgesetz f(x) = x2 - x + 2 verwendet, so erhält man folgende Wertetabelle:
| x | f(x) |
|---|---|
| 1 | f(1) = 2 |
| 2 | f(2) = 4 |
| 3 | f(3) = 8 |
| 4 | f(4) = 14 |
In diesem Fall lautet also die "logische" Fortsetzung 14.
Allgemein kann die - endliche - Zahlenfolge <2, 4, 8, a, ...> mit Hilfe des Bildungsgesetzes
f(x) = (a/6 - 7/3)x3 + (15 - a)x2- (11a/6 - 80/3)x + (16 - a)
erzeugt werden.
Damit können beispielsweise folgende Zahlenreihen gebildet werden:
| Zahlenreihe | Bildungsgesetz |
|---|---|
| <2, 4, 8, 10, ...> | f(x) = (-2/3)x3 + 5x2 - (25/3)x + 6 |
| <2, 4, 8, 11, ...> | f(x) = (-1/2)x3 + 4x2 - (13/2)x + 5 |
| <2, 4, 8, 14, ...> | f(x) = x2 - x + 2 |
| <2, 4, 8, 15, ...> | f(x) = (1/6)x3 + (5/6)x + 1 |
Sollen nun weitere Folgenglieder einer bestimmten Gesetzmäßigkeit gehorchen, so muß der Grad des Bildungsgesetzes erhöht werden, d.h. z. B. eine Funktion der Form f(x) = ax4 + bx3 + cx2 + dx + e, ... entwickelt werden.
So kann etwa für die Zahlenfolge <2, 4, 8, 16, a, ...> das Bildungsgesetz
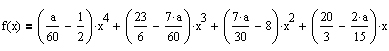
verwendet werden.
Auch die eingangs zitierte Zahlenfolge kann mit Hilfe einer Polynomfunktion erzeugt werden. In diesem Fall wird die Funktion f(x) = 2x in eine Potenzreihe entwickelt, d.h. es gilt: