Schüttung eines Brunnens
Ein Hausbesitzer ärgert sich über die ständigen Preiserhöhungen seines Leitungswassers. So bohrt er sich im späten Frühjahr einen Brunnen in seinem Garten und pumpt aus diesem täglich die maximal mögliche Wassermenge ab. Voller Verwunderung muss er feststellen, dass die Schüttung seines Brunnens keineswegs konstant ist und der trockene Sommer zu einer schnellen Abnahme der täglich förderbaren Wassermenge führt. Trotz der verspätet einsetzenden Niederschläge versiegt seine teure Anschaffung nach 100 Tagen, um kurzzeitig danach erneut zu sprudeln.
Der gute Vorsatz, die tägliche Schüttung zu notieren, verblasst relativ rasch im Alltag, weshalb nur sporadische Aufzeichnungen des täglich geförderten Wasservolumens existieren.
| Tag | Wassermenge (in l) |
|---|---|
| 0 | 3000 |
| 10 | 2916 |
| 27 | 2462 |
| 32 | 2275 |
| 40 | 1944 |
| 51 | 1455 |
| 68 | 725 |
| 90 | 84 |
| 100 | 0 |
| 120 | 408 |
Um den Schüttungsverlauf des errichteten Brunnens im Intervall [0; 100] besser erfassen zu können, werden weitere Daten benötigt. Diese können etwa durch das mathematische Modell einer kubischen Regressionskurve der Form f(x) = ax3 + bx2 + cx + d ermittelt werden.
Dazu werden die vorhandenen Daten in eine Excel-Tabelle eingegeben und in einem x-y-Diagramm dargestellt (dabei bezeichnet x den Tag nach Beginn der Aufzeichnungsreihe und y die am Tag x geförderte Wassermenge).
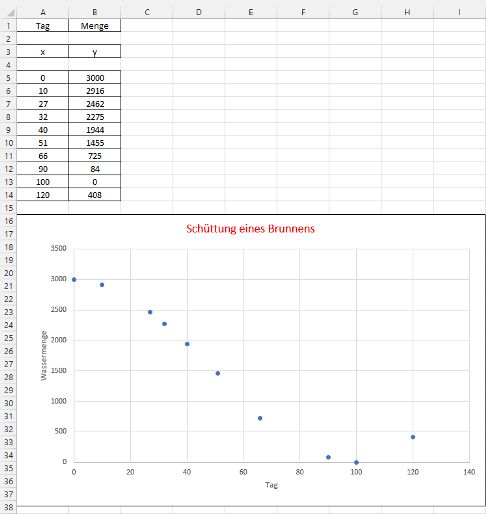
Nun wird dem bestehenden Schaubild eine Trendlinie vom Typ "Polynomisch" und vom Grad 3 hinzugefügt. Da die zu berechnenden Parameter a, b, c und d der kubischen Ausgleichsfunktion f(x) nicht direkt als Zellbezüge verfügbar sind, wird die ursprüngliche Tabelle um zwei Spalten mit den Einträgen x2 und x3 erweitert.
Anschließend wird die Excel-Funktion RGP auf die y-Werte D5 bis D14 und die x-Werte A5 bis C14 angewendet und das Ergebnis in den Zellen F5 bis I5 gespeichert. Zwecks besserer Übersicht werden die Inhalte der Zellen F5 bis I5 in die Zellen H8 bis H11 kopiert.
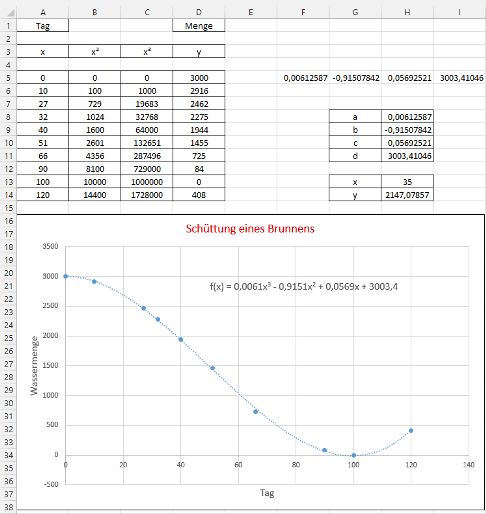
Damit kann innerhalb des Datenbereiches [0; 100] ein Schätzwert y (Zelle H14) für die zu erwartende Wasserfördermenge eines Tages x (Zelle H13) bzw. eine Trendprognose für den Schüttungsverlauf eines Zeitraumes [x; x + h] berechnet werden.