Dynamische Renten
Das Kernstück der Finanzmathematik ist die Werteberechnung von Renten, wobei die "klassische" Definition einer Rente besagt:
"Eine Rente ist eine Folge von Zahlungen in gleicher Höhe und in gleichen Zeitabständen."
Im TKP Excel finden sich zahlreiche finanzmathematische Funktionen, deren Parameter in folgender Tabelle wiedergegeben werden:
| BW | Barwert, Anfangskapital |
| F | Fälligkeit (0 für vorschüssig, 1 für nachschüssig) |
| RMZ | Regelmäßige Zahlung, Höhe einer Rentenrate |
| Zins | Zinssatz pro Zinsperiode |
| ZW | Zielwert, Endkapital |
| ZZR | Zahlungszeitraum, Gesamtzahl der Rentenraten |
Damit können folgende, in der Rentenrechnung häufig vorkommende, Funktionen verwendet werden:
| BW(Zins; ZZR; RMZ; ZW; F) | für den Barwert einer Rente |
| ZW(Zins; ZZR; RMZ; BW; F) | für den Endwert einer Rente |
Zinseszins- und Rentenrechnung sind − finanzmathematische − Anwendungen arithmetischer und geometrischer Folgen und Reihen, weshalb Bar- und Endwerte "klassischer" Renten neben den Excel-Bausteinen BW und ZW auch mit Hilfe von Arrays ermittelt werden können.
Da die Arrayformel {=ZEILE(1:n)} eine Zahlenfolge der ersten n natürlichen Zahlen erzeugt und ferner in jeder arithmetischen Folge die Differenz d und in jeder geometrischen Folge der Quotient q zweier aufeinander folgender Glieder konstant ist, gelten die Arrayformeln:
| {=(ZEILE(1:n)-1)*d+a1} | für die ersten n Glieder einer arithmetischen Folge mit dem Anfangsglied a1 und der Differenz d |
| {=q^(ZEILE(1:n)-1)*b1} | für die ersten n Glieder einer geometrischen Folge mit dem Anfangsglied b1 und dem Quotienten q |
Die für die Rentenrechnung relevante Reihenberechnung erhält man über
| {=SUMME((ZEILE(1:n)-1)*d+a1)} | für die n-te Partialsumme einer arithmetischen Reihe |
| {=SUMME(q^(ZEILE(1:n)-1)*b1)} | für die n-te Partialsumme einer geometrischen Reihe |
Somit ergeben sich unter Verwendung der Hilfsfunktion Länge=ZEILE(INDIREKT("1:"&n)) folgende Arrayformeln für Bar- und Endwert "klassischer" Renten:
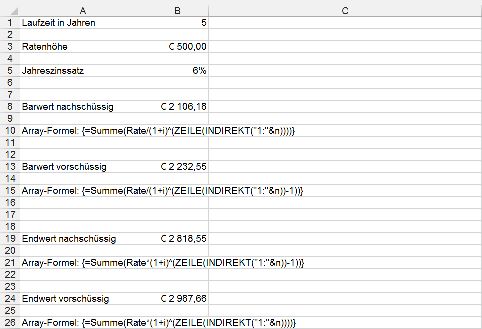
Die finanzmathematischen Funktionen BW und ZW können nur auf "klassische" Renten mit konstanter Ratenhöhe während der gesamten Laufzeit angewendet werden.
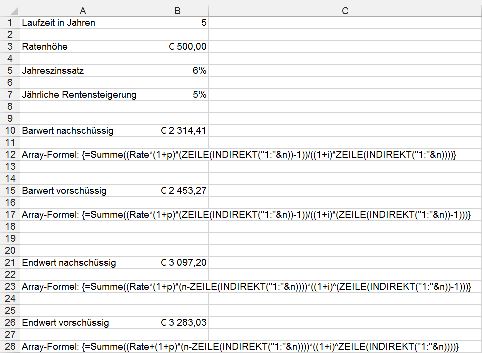
Wird allerdings eine Rente dynamisch, indem sie pro Rentenperiode um einen fixen Wert (z.B. € 30,--) oder um einen Prozentbetrag (etwa 5 %) erhöht wird, so ermöglicht eine kleine Veränderung der obigen Arrayformeln auch in diesem Fall eine Berechnung der jeweiligen Bar- und Endwerte.
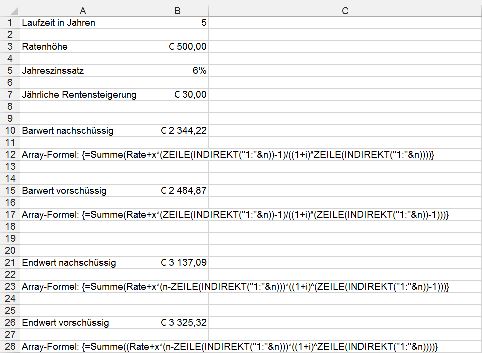
So erhält man etwa für eine dynamische Rente, bei der jede folgende Rate um x = € 30,-- höher als die jeweils vorangegangene Rate ist:
Und für eine dynamische Rente, bei der jede folgende Rate um p = 5 % höher als die jeweils vorangegangene ist, gilt: