Leonardo Fibonacci
Der Italiener Leonardo da PISA (ca. 1180 - 1250) - er selbst nannte sich Filius Bonacci, weshalb er heute vorwiegend als Fibonacci bekannt ist - war einer der berühmtesten Mathematiker des Mittelalters. Er fasste 1202 in seinem Buch Liber abaci, das heute nur noch in der neueren Version von 1228 erhalten ist, fast vollständig das Wissen über Arithmetik und Algebra der damaligen Zeit zusammen. Durch dieses Buch wurden in Westeuropa die heute noch verwendeten "arabischen" Ziffern bekannt, weshalb es für die weitere Entwicklung der Mathematik in den folgenden Jahrhunderten eine wichtige Bedeutung besaß.
Auf den Seiten 123 und 124 des Liber abaci findet sich folgende - hier nur sinngemäß wiedergegebene - berühmte Aufgabenstellung:
"Ein Paar neugeborener Kaninchen wirft nach zwei Monate ein neues Paar und in allen folgenden Monaten ein weiteres Paar. Wie viele Kaninchenpaare sind nach einem Jahr vorhanden, wenn kein Todesfall eintritt und sich jedes neue Paar auf die gleiche Art wie das ursprüngliche Paar vermehrt ?"
Die Zahlenfolge <1; 1; 2; 3; 5; 8; ...> liefert die Lösung, wobei jede Zahl größer 1 die Summe der beiden vorangegangenen Zahlen darstellt.
Stirbt also innerhalb des ersten Jahres kein Kaninchen, so gibt es nach zwölf Monaten genau 144 Kaninchenpaare.
Die Suche nach einer Formel, mit der man jedes (beliebige) Glied der Fibonacci-Folge explizit, d.h. ohne die Kenntnis der vorhergehenden Folgenglieder, berechnen kann, dauerte mehrere Jahrhunderte.
Schließlich veröffentlichte der französische Mathematiker Jacques Binet (1786-1856) im Jahre 1843 folgende Formel:
Das n-te Element an der Fibonacci-Folge <1; 1; 2; 3; 5; 8; ...> kann mit der Hilfe der Formel
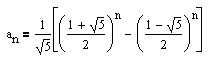
direkt berechnet werden.
Um diese Formel herzuleiten, erweitert man zunächst die Fibonacci-Folge um das Folgenglied a0 = 0 und schreibt anstelle der Beziehung
Mit Hilfe der (trivialen) Gleichung an = an + 0 ⋅ an - 1 sowie der Rechenregeln für die Multiplikation von Matrizen ergibt sich somit
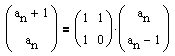.Bezeichnet man die Matrix
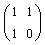mit A,so erhält man für die ersten drei Fibonacci-Folgenglieder
die Gleichungen
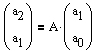und
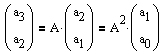.Für die beiden Folgenglieder an und an + 1 entsteht daher die Gleichung
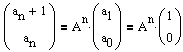.Besitzt nun eine Matrix die Gestalt einer Diagonalmatrix (d.h. alle Elemente außerhalb der Hauptdiagonale sind Null), so kann die n-te Potenz dieser Matrix durch Potenzieren jedes einzelnen Matrixelementes direkt gebildet werden.
Um nun die Matrix A auf eine Diagonalform zu bringen und somit die Matrix An möglichst effektiv berechnen zu können, ist ein kleiner Ausflug in die Welt der linearen Algebra nötig.
Kenner der Kegelschnitte wissen, daß die Gleichung einer Ellipse in erster Hauptlage mit den Achsenlängen a = 4 und b = 2
x2 + 4y2 = 16
lautet.
Diese Gleichung kann mit Hilfe von Vektoren und Matrizen auch in der Form
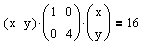
angeschrieben werden.
Dreht man nun diese Ellipse im rechten Winkel gegen den Uhrzeigersinn, so benötigt man neben der Drehmatrix
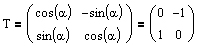
auch deren inverse Matrix
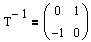.Mit Hilfe des Ansatzes
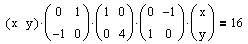
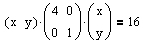
erhält man eine Ellipse in zweiter Hauptlage.
Analog ergibt sich für eine Drehung um einen Winkel von 30 Grad gegen den Uhrzeigersinn:
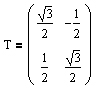und
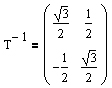
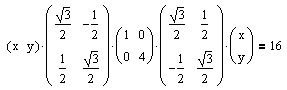
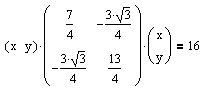
Die gesuchte Gleichung lautet also 7x2 − 6 ⋅ (√(3))xy + 13y2 = 64.
In diesem Fall ist aus der ursprünglichen Diagonalmatrix
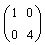die symmetrische Matrix 
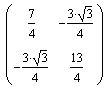entstanden.Für die Entwicklung einer Formel, mit der jedes Element der Fibonacci-Folge explizit (direkt) berechnet werden kann, ist nun die umgekehrte Richtung, d.h. die Entwicklung einer Diagonalmatrix aus einer symmetrischen Matrix, von Bedeutung.
Ausgehend von der Matrix A, die durch die Multiplikation
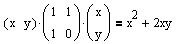
zur Gleichung einer Hyperbel in allgemeiner Lage führt, wird zuerst unter Verwendung der Einheitsmatrix die (charakteristische) Gleichung
det(A - λE) = λ2 − λ − 1 = 0
gelöst.
Die beiden Lösungen
λ1 = (1 + √(5))/2 und λ2 = (1 − √(5))/2
sind bereits die Einträge der gesuchten Diagonalmatrix
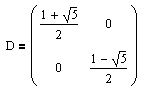.Um nun die noch fehlenden (Dreh-)Matrizen T und T -1 zu erhalten, werden die Lösungsmengen (x1/y1) und (x2/y2) der beiden Gleichungssysteme
(A - λ1E)(x y)T = 0 bzw. (A - λ2E) (x y)T = 0
ermittelt.
Da jedes der beiden Gleichungssysteme unterbestimmt ist, können zunächst die beiden Vektoren
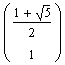und
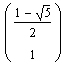
als Basis angegeben werden.
Setzt man jedoch zusätzlich voraus, daß jeder der beiden Vektoren die Länge 1 besitzt, so erhält man zum einen die beiden Einheitsvektoren
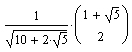und
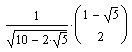
und zum anderen die Drehmatrix
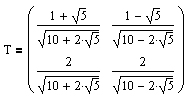.Betrachtet man die Komponenten der Drehmatrix T genauer, so zeigt sich, dass es sich bei den eingetragenen Werten um die Werte von sin 31,71º bzw. cos 31,71º handelt.
Dies bedeutet, daß die Hyperbel mit der Gleichung x2 + 2xy = 1 durch Drehung der Hyperbel x2 - y2 = 1 (erste Hauptlage) um rund 31,71º gegen den Uhrzeigersinn entstanden ist.
Für die eingangs festgelegte Matrix A gilt daher die Gleichung
D = T-1 ⋅ A ⋅ T bzw. A = T ⋅ D ⋅ T-1
und weiters
A2 = (T ⋅ D ⋅ T-1) ⋅ (T ⋅ D ⋅ T-1) = (T ⋅ D) ⋅ (T-1 ⋅ T) ⋅ (D ⋅ T-1) = T ⋅ D2 ⋅ T-1
bzw.
An = T ⋅ Dn ⋅ T-1.
Mit Hilfe der Gleichung
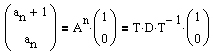
erhält man
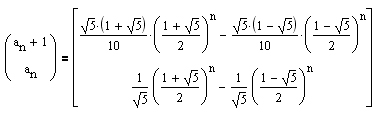
und somit
.
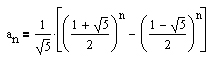