Nachbarn beim Lotto
Bei der Ziehung der Lottozahlen stellt so manche*r Spielteilnehmer*in fest, daß getreu dem Motto "Knapp daneben ist auch vorbei." eine oder mehrere der sechs Gewinnzahlen auf dem Spielschein unmittelbar neben einer der sechs getippten Zahlen liegt bzw. liegen.
Und bei Betrachtung der Ziehungsergebnisse mehrerer aufeinander folgender Lottorunden zeigt sich nicht selten, daß unter den sechs Gewinnzahlen zumindest zwei aufeinander folgende Zahlen sind.
Aber:
"Wie groß ist tatsächlich die Wahrscheinlichkeit, daß unter den sechs Gewinnzahlen einer Lottoziehung keine zwei Zahlen benachbart sind ?"
Um diese Wahrscheinlichkeit zu berechnen, ist ein kleiner Griff in die Trickkiste nötig:
Wenn unter den sechs numerisch aufsteigend geordneten Gewinnzahlen
1 ≤ x1 < x2 < x3 < x4 < x5 < x6 ≤ 45
einer Lottoziehung keine zwei aufeinander folgenden Gewinnzahlen benachbart sein dürfen, so müssen sie sich um mindestens zwei Einheiten unterscheiden, d.h. es muß
xi < xi + 1 − 1
gelten.
Für die eingangs aufsteigend geordneten Gewinnzahlen erhält man dadurch die Bedingung
1 ≤ x1 < x2 − 1 < x3 − 2 < x4 − 3 < x5 − 4 < x6 − 5 ≤ 40.
Somit bleibt die Frage, wie viele Ziehungsergebnisse der Form {y1, y2, y3, y4, y5, y6} mit der Eigenschaft
1 ≤ y1 < y2 < y3 < y4 < y5 < y6 ≤ 40
gebildet werden können.
Da die Antwort auf diese Frage
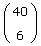lautet, erhält man für die Wahrscheinlichkeit, daß unter den sechs Gewinnzahlen einer Lottoziehung keine zwei Zahlen benachbart sind,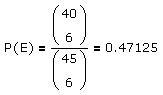
d.h. es ist bei jeder (!) Lottoziehung eher damit zu rechnen, daß zumindest zwei der sechs Gewinnzahlen benachbart sind.
Und wie groß ist nun die Wahrscheinlichkeit, daß unter den sechs Gewinnzahlen einer Lottoziehung genau zwei, drei, ... Gewinnzahlen benachbart sind ?
Bei der Klärung dieser Frage startet man am einfachsten mit dem Fall, daß alle sechs Gewinnzahlen benachbart sind.
Hier gibt es die insgesamt 40 Möglichkeiten von {1, 2, 3, 4, 5, 6} bis {40, 41, 42, 43, 44, 45}, sodaß
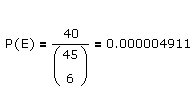
gelten muss.
Die soeben berechnete Wahrscheinlichkeit kann aber auch durch Modifizieren des weiter oben vorgestellten Modells
1 ≤ x1 < x2 − 1 < x3 − 2 < x4 − 3 < x5 − 4 < x6 − 5 ≤ 40
ermittelt werden.
Da nämlich bei sechs benachbarten Gewinnzahlen die fortgesetzte Gleichung
x6 = x5 + 1 = x4 + 2 = x3 + 3 = x2 + 4 = x1 + 5
gelten muss, reduziert sich das Modell
1 ≤ x1 < x2 − 1 < x3 − 2 < x4 − 3 < x5 − 4 < x6 − 5 ≤ 40
auf die Bedingung
1 ≤ x1 ≤ 40,
da mit der ersten Gewinnzahl x1 auch alle anderen Gewinnzahlen x2 bis x6 eindeutig bestimmt sind.
Und da es trivialerweise
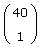Möglichkeiten gibt, eine Zahl aus insgesamt 40 Zahlen auszuwählen, erhält man die bereits angegebene Formel.Ähnlich verhält es sich mit den übrigen Fällen, die im folgenden tabellarisch aufgelistet sind:
Fünf benachbarte Gewinnzahlen:
| Benachbarte Gewinnzahlen | Gesuchte Zahlen | Anzahl |
|---|---|---|
| x1, x2, x3, x4, x5 | x1, x6 |  |
| x2, x3, x4, x5, x6 | x1, x2 | |
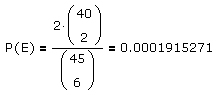
Vier benachbarte Gewinnzahlen:
| Benachbarte Gewinnzahlen | Gesuchte Zahlen | Anzahl |
|---|---|---|
| x1, x2, x3, x4 | x1, x5, x6 |  |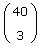
| x2, x3, x4, x5 | x1, x2, x6 | |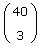
| x3, x4, x5, x6 | x1, x2, x3 | |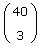
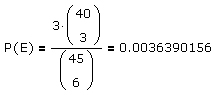
Einmal vier und einmal zwei benachbarte Gewinnzahlen:
| Benachbarte Gewinnzahlen | Gesuchte Zahlen | Anzahl |
|---|---|---|
| x1, x2, x3, x4 sowie x5, x6 | x1, x5 | |
| x3, x4, x5, x6 sowie x1, x2 | x1, x3 | |
Drei benachbarte Gewinnzahlen:
| Benachbarte Gewinnzahlen | Gesuchte Zahlen | Anzahl |
|---|---|---|
| x1, x2, x3 | x1, x4, x5, x6 |  |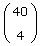
| x2, x3, x4 | x1, x2, x5, x6 |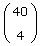
|
| x3, x4, x5 | x1, x2, x3, x6 | |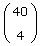
| x4, x5, x6 | x1, x2, x3, x4 | |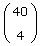
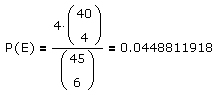
Zweimal drei benachbarte Gewinnzahlen:
| Benachbarte Gewinnzahlen | Gesuchte Zahlen | Anzahl |
|---|---|---|
| x1, x2, x3 sowie x4, x5, x6 | x1, x4 | |
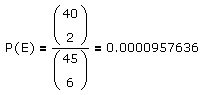
Einmal drei und einmal zwei benachbarte Gewinnzahlen:
| Benachbarte Gewinnzahlen | Gesuchte Zahlen | Anzahl |
|---|---|---|
| x1, x2, x3 und x4, x5 | x1, x4, x6 | |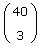
| x1, x2, x3 und x5, x6 | x1, x4, x5 | |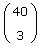
| x2, x3, x4 und x5, x6 | x1, x2, x5 | |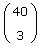
| x3, x4, x5 und x1, x2 | x1, x3, x6 | |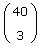
| x4, x5, x6 und x1, x2 | x1, x3, x4 | |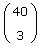
| x4, x5, x6 und x2, x3 | x1, x2, x4 | |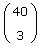
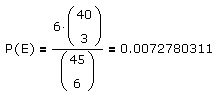
Einmal zwei benachbarte Gewinnzahlen:
| Benachbarte Gewinnzahlen | Gesuchte Zahlen | Anzahl |
|---|---|---|
| x1, x2 | x1, x3, x4, x5, x6 |  |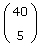
| x2, x3 | x1, x2, x4, x5, x6 | |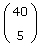
| x3, x4 | x1, x2, x3, x5, x6 | |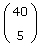
| x4, x5 | x1, x2, x3, x4, x6 | |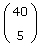
| x5, x6 | x1, x2, x3, x4, x5 | |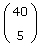
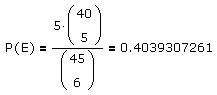
Zweimal zwei benachbarte Gewinnzahlen:
| Benachbarte Gewinnzahlen | Gesuchte Zahlen | Anzahl |
|---|---|---|
| x1, x2 und x3, x4 | x1, x3, x5, x6 | |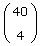
| x1, x2 und x4, x5 | x1, x3, x4, x6 | |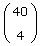
| x1, x2 und x5, x6 | x1, x3, x4, x5 | |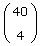
| x2, x3 und x4, x5 | x1, x2, x4, x6 | |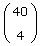
| x2, x3 und x5, x6 | x1, x2, x4, x6 | |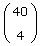
| 3, x4 und x5, x6 | x1, x2, x3, x5 | |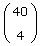
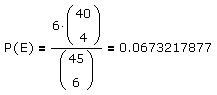
Dreimal zwei benachbarte Gewinnzahlen:
| Benachbarte Gewinnzahlen | Gesuchte Zahlen | Anzahl |
|---|---|---|
| x1, x2 sowie x3, x4 und x5, x6 | x1, x3, x5 | |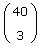
