Um den Äquator 02
Wie sehr sich eine kleine Änderung der Aufgabenstellung auf den Wert des Ergebnisses auswirken kann, zeigt diese Folge.
Zunächst wiederum die Aufgabenstellung:
Ein Seil wird straff um den Erdäquator gespannt und anschließend um 1 Meter verlängert.
Bis zu welcher Seehöhe muss das Seil an einer Stelle hochgezogen werden, damit es wieder gespannt wird, wenn für die Erdgestalt vereinfacht eine Kugel mit einem Radius von 6370 km angenommen wird ?
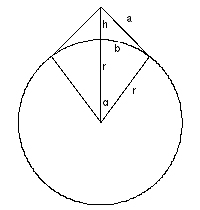
Bezeichnet man die gesuchte Seehöhe mit h, den Radius der Erdkugel mit r, den Abstand Seilspitze-Berührpunkt mit a, die Enfernung Fußpunkt unter der Seilspitze-Berührpunkt mit b und mit α den Winkel zwischen den Verbindungslinien Erdmittelpunkt-Seilspitze sowie Erdmittelpunkt-Berührpunkt, so gelten:
tan(α) = (a/r)
und
α = (b/r)
Wird die zweite Gleichung von der ersten subtrahiert, so ergibt sich:
tan(α) - α = (a/r) − (b/r) = (a − b)/r
Anhand der Skizze ist die Beziehung 2b + 1 = 2a erkennbar, somit gilt
a − b = (1/2)
und damit
tan(α) − α = 1/(2r) bzw. tan(α) − α − 1/(2r) = 0.
Da diese Gleichung nicht analytisch aufgelöst werden kann, wird eine numerische Lösung ermittelt. Bei Anwendung des NEWTON´schen Näherungsverfahrens erhält man für den Startwert α = 0,174533 (1 Grad) und die Funktionen
f(α) = tan(α) − α − 1/(2r) bzw. f´(α) = 1/(cos2(α)) − 1 die Tabelle:
| α | f(α) | f´(α) | α − (f(α)/f´(α)) |
|---|---|---|---|
| 0,174533 | 0,0000017 | 0,0003047 | 0,0118936 |
| 0,0118936 | 0,0000005 | 0,0001415 | 0,0084841 |
| 0,0084841 | 0,0000001 | 0,0000455 | 0,0062222 |
| 0,0062222 | 0,0000000 | 0,0000387 | 0,0061755 |
| 0,0061755 | 0,0000000 | 0,0000381 | 0,0061752 |
| 0,0061752 | 0,0000000 | 0,0000381 | 0,0061752 |
Der Winkel α beträgt somit rund 0,3536628°.
Aus der Beziehung
cos(α) = r/(r + h)
erhält man durch Umformen die Gleichung
h = r/cos(α) − r = 121,505 m.
Das um 1 Meter verlängerte Seil muß also an einer Stelle rund 121,205 Meter hochgezogen werden, damit es wieder gespannt ist.