Vertauschte Briefe
Eine Sekretärin schreibt fünf Briefe (mit verschiedenem Inhalt) und adressiert fünf Umschläge (mit verschiedenen Adressen). Anschließend steckt sie jeweils einen Brief − ohne auf die jeweilige Adresse zu achten − willkürlich in einen (noch leeren) Umschlag.
Wie groß ist die Wahrscheinlichkeit, daß mindestens ein Brief in den richtigen Umschlag gelangt ?
Bezeichnet man mit an die Anzahl der Möglichkeiten, daß bei n Briefen und n Umschlägen kein Brief im richtigen Umschlag landet, so gelten
a1 = 0 (ein Brief landet bei einem Umschlag stets in diesem)
und
a2 = 1 (bei zwei Briefen und zwei Umschlägen gibt es eine richtige und eine falsche Variante).
Für die Zahlen a3 und a4 gelten folgende Tabellen:
| Umschlag | 1 | 2 | 3 |
|---|---|---|---|
| Brief | 3 | 1 | 2 |
| 2 | 3 | 1 |
| Umschlag | 1 | 2 | 3 | 4 |
|---|---|---|---|---|
| Brief | 2 | 1 | 4 | 3 |
| 3 | 1 | 4 | 2 | |
| 4 | 1 | 2 | 3 | |
| 2 | 4 | 1 | 3 | |
| 3 | 4 | 1 | 2 | |
| 4 | 3 | 1 | 2 | |
| 2 | 3 | 4 | 1 | |
| 3 | 4 | 2 | 1 | |
| 4 | 3 | 2 | 1 |
Es gelten somit a3 = 2 und a4 = 9, wobei der Wert 9 für die Variable a4 auch durch folgende Überlegung erhalten werden kann:
Betrachtet man zunächst jene Fälle, in denen Brief 1 in Umschlag 2 landet, so kann folgende Unterscheidung durchgeführt werden:
Steckt Brief 1 in Umschlag 2 und Brief 2 in Umschlag 1, so können die restlichen 4 − 2 = 2 Briefe auf a2 = 1 Art den verbleibenden 4 − 2 = 2 Umschlägen falsch zugeteilt werden.
Steckt jedoch Brief 1 in Umschlag 2 und Brief 2 nicht in Umschlag 1, so können die drei Briefe 2, 3 und 4 den drei verbleibenden Umschlägen 1, 3 und 4 auf genau a3 = 2 Arten falsch zugeordnet werden (und zwar genau dann, wenn Brief 2 nicht in Umschlag 2, Brief 3 nicht in Umschlag 3 und Brief 4 nicht in Umschlag 4 landen).
Die bisherige Gesamtzahl a3 + a2 muß nun noch mit 3 multipliziert werden, da Brief 1 (fälschlicherweise) nicht nur in Umschlag 2, sondern auch in Umschlag 3 oder in Umschlag 4 gelangen kann.
Es gilt daher
a4 = 3 ⋅ (a3 + a2)
und in Verallgemeinerung
an = (n − 1) ⋅ (an - 1 + an − 2).
Für die gesuchte Wahrscheinlichkeit benötigt man daher zum einen die Formel a5 = 4 ⋅ (a4 + a3) und zum anderen die Tatsache, daß fünf Briefe fünf Umschlägen auf genau 5! = 120 Arten willkürlich zugeordnet werden können.
Damit ergibt sich:
P(E) = 1 − (44/120) = (19/30).
Und wie groß ist die Wahrscheinlichkeit, daß genau (0 ≤) k (≤ 5) Briefe im jeweils richtigen Kuvert landen ?
Trivialerweise gibt es bei fünf Briefen und fünf Umschlägen genau eine Möglichkeit, daß alle fünf Briefe im jeweils richtigen Kuvert landen (d.h. P(X = 5) = (1/5!)), und zugleich keine Möglichkeit, daß genau vier der fünf Briefe in den richtigen Umschlag gesteckt werden (d.h. P(X = 4) = 0).
Für die Wahrscheinlichkeiten P(X = 0) bis P(X = 3) gilt:
Es gibt genau
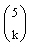Möglichkeiten, daß von fünf Briefen genau k Briefe im richtigen Umschlag sind, zugleich können die restlichen 5 − k Briefe auf genau a5 − k Arten in einen falschen Umschlag gelegt werden.Damit erhält man für 0 ≤ k ≤ 3:
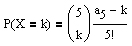
Die Zufallsvariable X = "Anzahl der Briefe im richtigen Umschlag" besitzt also folgende Verteilung:
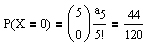
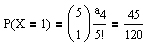
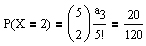
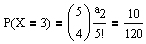
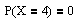
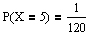
Bleibt zum Schluß dieses Artikels noch die allgemeine Fragestellung:
Wie groß ist die Wahrscheinlichkeit, daß bei n Briefen und n Umschlägen genau (0 ≤) k (≤ n) Briefe im jeweils richtigen Kuvert landen ?
Hier ist es günstig, zuerst eine explizite Darstellung für die Zahl an (Möglichkeiten, daß keiner der n Briefe im jeweils richtigen Kuvert landet) zu entwickeln.
Aus den Formeln a3 = 2 ⋅ (a2 + a1), a4 = 3 ⋅ (a3 + a2) und a5 = 4 ⋅ (a4 + a3) erhält man durch Umformen bzw. Ergänzen:
| a3 = 2 ⋅ (a2 + a1) | a3 − 2 ⋅ a2 = 2a1 | a3 − 3 ⋅ a2 = − a2 + 2a1 |
| a4 = 3 ⋅ (a3 + a2) | a4 − 3 ⋅ a3 = 3a2 | a4 − 4 ⋅ a3 = − a3 + 3a2 |
| a5 = 4 ⋅ (a4 + a3) | a5 − 4 ⋅ a4 = 4a3 | a5 − 5 ⋅ a4 = − a4 + 4a3 |
Nun gilt etwa
a5 − 5 ⋅ a4 = − a4 + 4a3 = − (− a3 + 3a2) = − (− (− a2 + 2a1)) = − a2 + 2a1 = −1
und in Verallgemeinerung:
an − n ⋅ an − 1 = − an − 1 + (n − 1).an − 2 = (−1)[an − 1 − (n − 1) ⋅ an − 2] =
= (−1)2[an − 2 − (n − 2).an − 3] = ... = (−1)n − 2(a2 − 2a1 = (−1)n − 2 = (−1)n
Daraus erhält man die Gleichung
an − n ⋅ an − 1 = (−1)n,
welche durch Umformung und anschließende Division durch n! in die Gleichung
bzw.
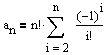
übergeht.
Setzt man nun 0! = 1, so kann die letzte Gleichung aufgrund der Summengleichheit
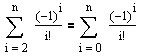
auch in der Form
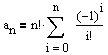
dargestellt werden.
Für die Berechnung der Wahrscheinlichkeit P(X = k), daß bei n Briefen und n Umschlägen genau (0 ≤) k (≤ n) Briefe im jeweils richtigen Kuvert landen, gilt daher:
Es gibt genau
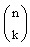Möglichkeiten, daß exakt k Briefe in das richtige Kuvert gelangen und genau an − k Möglichkeiten, daß jeder der restlichen n − k Briefe in einen falschen Umschlag gesteckt wird.Da alle n Briefe den n Umschlägen prinzipiell auf n! Arten zugeteilt werden können, erhält man somit:
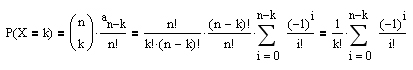
Dabei gelten insbesondere
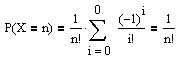
und
.
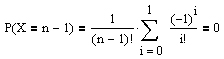